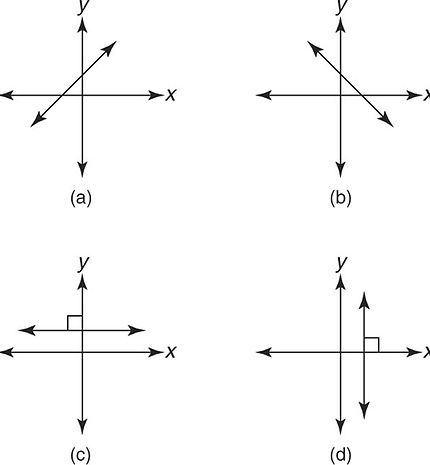
Slope

​Slope is the rise or drop of a line.

​

• ​The problems from this picture is that with out it having a positive slope (A), it would probably be a straight line (C)(slope of 0), a vertical line (D) (undefined slope), or a negative slope (B)(falls from left to right).
• This object, as I already stated, has a positive slope.
• ​The way to find the slope of a line in a coordinate plane with the coordinates of two lines is to plug them into the slope formula:       y2- y1

                                                 M=  --------------

                                                            x2 - x1

​

For example: A (-4, 8) , B (2, -6) the (-4) is ​​​x1 and the 2 is y1.

​

The 8 is x2 and the (-6) is ​ y2​. Plug them into the formula and

do the math. Then graph the equation by using the slope-intercept formula: y= mx + b whereas m=the slope, the example is above ^. In order to do this, you must find what y ( b in the slope-intercept formula) equals and x (which is x in the slope-intercept formula). There will be an equation for you to use in  order to solve for the problem and graph it. ​

For example: 10= m(4) + b.

In order to solve this you must find the slope and plug it into the formula.

The slope for this problem be 2.

10= 2(4)+b

Now you have to find b.

10= 8+b        Distributive Property.

10= 8+b        Subtraction Property.

-8   -8

---------

2= b              Solution.

​

To graph this you must plug in the y -intercept(b) and

plot it on the coordinate plane then use the slope

which was 2 to plot the next point, to do this you

will use the rise/run technique which is to rise up 2,

you only  go down on the rise if and only if the

slope is negative, and run, to go over to the right, 1, you

only go to the left if and only if this part of the slope is

negative.

​

To learn some more about slope, watch the video below: